
Error de medición del diámetro del
fuste de Guazuma crinita con forcípula, cinta métrica y cinta diamétrica,
Ucayali, Amazonia Peruana
Error of measurement of the diameter
of the stem of Guazuma crinita with forceps, metric belt and diametric belt,
Ucayali, Peruvian Amazon
Octavio Francisco Javier Galván
Gildemeiste
Universidad
Nacional Intercultural de la Amazonia, Perú
ogalvang@unia.edu.pe
Diana Isabel Torres Neyra
Universidad Nacional Intercultural de
la Amazonia, Perú
diana_torresneyra@hotmail.com
Luis Alejandro Rodríguez García
Universidad Nacional Intercultural de
la Amazonia, Perú
luroga66@hotmail.com
Erasmo Andrés Rosado Orneta
Regente forestal, Perú
sirf2012@hotmail.com
RESUMEN
El aumento de las plantaciones
con fines comerciales de Guazuma crinita, una especie prominente en la
Amazonia peruana, requiere que se mejoren las mediciones de los árboles para la
cuantificación del volumen de madera. Esta investigación tuvo como objetivo
determinar el error en la medición del diámetro normal del fuste (dap) y en el
cálculo del volumen, cuando el diámetro normal del fuste se mide con cinta
métrica, cinta diamétrica y forcípula de aluminio. Se midieron 41 árboles de
una plantación forestal de Guazuma crinita, de 13 años, en la zona de
Pucallpa, Amazonia peruana. Con la forcípula se midieron dos diámetros y los
promedios se obtuvieron con la media aritmética y la media geométrica. La
irregularidad de la sección transversal de los fustes de los árboles fue
cercana a uno. El análisis descriptivo e inferencial encontró que la medición
de un dap, con una forcípula, se diferencia notablemente de los otros métodos y
genera el mayor error relativo, con 4 % para el diámetro normal y 7.9 % para el
volumen, a nivel de árbol. Pero, a nivel de hectárea, se encontró un error
absoluto de hasta 7.7 m3/ha, cifra importante desde la dimensión industrial y
financiera. Se concluyó que el diámetro normal se puede medir,
indiferentemente, con una cinta métrica, cinta diamétrica o mediante la media
de dos diámetros con una forcípula de aluminio. Además, se concluyó que es
indistinto usar la media aritmética o la media geométrica.
Palabras clave: Cinta
métrica, forcípula, diámetro normal del fuste, error absoluto, error relativo.
ABSTRACT
Increased
commercial plantations of Guazuma crinita, a prominent species in the Peruvian
Amazon, require improved tree measurements for wood volume quantification. The
objective of this research was to determine the error in the measurement of the
normal diameter of the stem (dbh) and in the calculation of the volume, when
the normal diameter of the stem is measured with a tape measure, a diameter
tape and an aluminum caliper. Forty-one trees from a 13-year-old Guazuma
crinita forest plantation were measured in the Pucallpa area, Peruvian Amazon.
Two diameters were measured with the caliper and the averages were obtained
with the arithmetic mean and the geometric mean. The irregularity of the cross
section of the stems of the trees was close to one. The descriptive and
inferential analysis found that the measurement of a dbh, with a caliper,
differs markedly from the other methods and generates the largest relative
error, with 4% for the normal diameter and 7.9% for the volume, at the tree
level. But, at the hectare level, an absolute error of up to 7.7 m3/ha was
found, an important quantity from the industrial and financial dimension. It
was concluded that the normal diameter can be measured, indifferently, with a
tape measure, diametric tape or through the average of two diameters with an
aluminum caliper. In addition, it was concluded that it is indistinct to use
the arithmetic mean or the geometric mean.
Keywords: Tape measure, caliper, normal stem diameter, absolute error,
relative error.
INTRODUCCIÓN
El aporte de las plantaciones a
las exportaciones peruanas es muy reducido, pues, en el año 2015, de los 1.69
millones de metros cúbicos de madera exportada 80 % provino de bosques
naturales y 20 % de plantaciones (SERFOR 2015); aunque la totalidad de
productos forestales importados provinieron de plantaciones (Guariguata et al.
2017). No obstante, en Perú se ha creado un marco legal más favorable para el
desarrollo de plantaciones, pues los inversionistas requieren la zonificación
de tierras aptas para plantaciones, vías de transporte, fábricas e innovación
permanente (Guariguata et al. 2017). Empero, no se cuenta con información
silvicultural y tecnológica completa para ninguna especie nativa (Guariguata et
al. 2017), por consiguiente se entiende que se carece de métodos validados para
la medición de los árboles. El diámetro es la medida de un árbol más factible
de medir (Soares et al. 2010, Rondeux 2010, Diéguez et al. 2003), se asegura la
precisión porque se mide directamente (Malleux 1982), sirve para cuantificar el
área basal, volumen, biomasa, etc. (Diéguez et al. 2003, Malleux 1982) y para
describir la estructura horizontal del bosque (Soares et al. 2010). El diámetro
más común de medir es el diámetro normal o diámetro a la altura del pecho
(dap), medido a 1.30 m sobre el nivel del suelo (López y Ambrosio 2009). Si se
va a medir el diámetro, para mermar el error se debe efectuar dos mediciones en
diferentes sentidos (Diéguez et al. 2003, Philip 1994) y, seguidamente, obtener
la media aritmética o la media geométrica (Diéguez et al. 2003). Pero también
es posible medir la circunferencia o sea la longitud del perímetro (Rondeux
2010, López y Ambrosio 2009, Diéguez et al. 2003, López y Marchal 1991). Cuando
la sección transversal del fuste es circular, la división de la circunferencia
entre 3.1416 (π) genera el diámetro, con la ventaja de que no hay una
dirección determinada para medirla (Diéguez et al. 2003). En el caso de las
plantaciones, se considera que la medición del diámetro y la circunferencia son
apropiados (Philip 1994). El diámetro se mide con la forcípula o la cinta
diamétrica (en realidad una cinta métrica con las longitudes divididas entre
π y la circunferencia con la cinta métrica (Soares et al. 2010, Diéguez et
al. 2003).
Existe el consenso de que la
cinta métrica es más precisa que la forcípula (Rondeux 2010, Silva et al. 2005,
Diéguez et al. 2003, Prodan et al. 1997, Alder y Synnott 1992, Synnott 1991 y
Cailliez 1980) lo cual se puede explicar porque la lectura es equivalente al
promedio de infinitos diámetros (Rondeux 2010), además la medición no es afectada
por la orientación de modo que es más consistente (Campos y Leite 2009) y
Rondeux 2010). Empero, la cinta métrica o la cinta diamétrica tienden a
sobrestimar el diámetro (Diéguez et al. 2003, Philip 1994, Avery y Burkhart
1994 y Cailliez 1980).
A pesar de lo mencionado antes,
estudios con especies tropicales indican que, estadísticamente, no hay
desigualdades entre la forcípula y la cinta métrica; es el caso de Cryptomeria
japónica con dap medio de 24 cm, en Rio Negro, Brasil (Corte et al. 2016), Toona
ciliata, con dap medio de 27.1 cm, y Swietenia macrophylla, con dap
medio de 19.8 cm; en sistemas agroforestales de Minas Gerais, Brasil (Costa et
al. 2018) y Pinus spp. con dap medio de 38.5 cm, medido y Eucalyptus
spp. con dap medio de 45.8 cm; en Piracicaba, Brasil (Freitas y Wichert
1998). No obstante, Wabö et al. (2007) si revelan diferencias la cinta
diamétrica y la forcípula en la medición de Nothofagus pumilio
(Provincia de Tierra del Fuego, Argentina) para árboles con dap de 10 cm a 80
cm.
Las contradicciones, antes
mencionadas, tal como afirma Masías (2017), podrían tener como causa que la
bibliografía clásica se refiere a resultados obtenidos en bosques templados.
En cuanto al precio de los
equipos, las diferencias son notables, pues los precios para la forcípula de
madera, forcípula de aluminio, cinta diamétrica de tela, cinta diamétrica de
metal y cinta métrica de plástico son de 50 Soles, 1 200 Soles, 220 Soles, 320
Soles y 5 Soles; respectivamente (para marzo del 2020, el cambio de un dólar americano
se cotizó en 3.4 Soles).
Entonces, es necesario comparar
el error de la cinta diamétrica, la cinta métrica y la forcípula; para el caso
de especies del trópico húmedo, como es el caso de Guazuma crinita. Con
base en lo descrito, esta investigación propuso como objetivos:
•
Determinar la precisión y el error de la cinta métrica, la cinta
diamétrica y la forcípula en la medición del diámetro normal y el cálculo del
volumen del fuste.
•
Evaluar la precisión y el error de la forcípula en la medición del diámetro
normal mediante la medición de uno o dos diámetros del fuste.
•
Evaluar la precisión y el error de la media aritmética y la media
geométrica en el cálculo del diámetro normal.
Se espera que esta investigación
sirva a los interesados en mediciones de crecimiento, producción o
productividad en plantaciones de Guazuma crinita “bolaina blanca” e,
inclusive, de otras especies nativas que se estén empleando en plantaciones o
que habiten en bosques secundarios.
MATERIALES Y MÉTODOS
Sitio de estudio
El estudio se realizó en una
plantación de Guazuma crinita de la Estación Experimental Agraria Pucallpa, del
Instituto Nacional de Innovación Agraria (Km. 3 Carretera Federico Basadre,
Pucallpa, Región Ucayali). Los árboles que se midieron tenían 13 años de edad y
una altura promedio de 17 metros. El sitio tiene una temperatura media de 28°C
y precipitación promedio anual de 1700 mm por año (UNU 2008); sobre una
fisiografía de terraza alta.
Mediciones de los árboles
El diámetro normal (dap) y la
circunferencia normal (cap) del fuste se midieron a 1.30 metros de la base del
fuste. Los diámetros se midieron con una cinta diamétrica metálica y una
forcípula de aluminio. La circunferencia se midió con una cinta métrica de
material sintético (comúnmente usadas en costura). Las mediciones se hicieron
en sentido perpendicular al fuste. Con la forcípula se midieron dos diámetros,
pero, con base en lo que sugieren Philip (1994) y Diéguez et al. (2003), se
midieron (sistemáticamente) dos diámetros perpendiculares entre sí, uno de
ellos paralelo al lado de la plantación. Las mediciones se hicieron en
centímetros, con redondeo al milímetro. Se consideró que la altura del fuste
fue la longitud desde la base del árbol hasta la base de la copa, para lo cual
se empleó un hipsómetro Blume Leiss.
Tratamientos y repeticiones
Los tratamientos fueron los
métodos mediante los que se obtuvieron los diámetros normales del fuste:
CM: dap que se obtuvo de la medición de la circunferencia con la
cinta métrica.
CD: dap que se midió con la cinta diamétrica.
FMA: dap que se obtuvo de la media aritmética de dos diámetros
medidos con la forcípula.
FMG: dap que se obtuvo de la media geométrica de dos diámetros
medidos con la forcípula.
F: un dap medido con la forcípula.
El diámetro que se midió con la
cinta métrica se reconoció como el diámetro normal real, porque la medición de
la circunferencia no se afecta por la dirección en que se mide el diámetro y el
cálculo del área basal es más preciso cuando se mide la circunferencia (Diéguez
et al. 2003). Se midieron los 41 árboles de la plantación, una muestra grande
que, por ser una cantidad superior a 30, permitió acogerse a la utilidad del
teorema del límite central.
Procesamiento de los datos
Los datos se archivaron
electrónicamente en una hoja de EXCEL, en la cual se hicieron los cálculos para
obtener los diámetros y volúmenes.
La sección transversal del fuste
de un árbol tiende a asemejarse a la de un círculo, empero, se concurre cierta
irregularidad o excentricidad (Diéguez et al. 2003, Prodan et al. 1997, Philip
1994, Cailliez 1980); por lo tanto, si la sección fuera cabalmente circular, el
cociente entre cualquiera de dos diámetros equivaldría a la unidad. La
irregularidad o excentricidad de la sección transversal del fuste se calculó
mediante la división entre dos dap, con el dap mayor como dividendo y el dap
menor como divisor.
De la circunferencia (cap) se
obtuvo el dap mediante la siguiente fórmula:
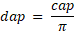
De Moya (2005)
se obtuvieron las fórmulas para calcular la media aritmética y la media
geométrica:
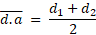
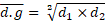
Donde: 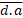 = media aritmética
= media aritmética
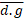 = media geométrica
= media geométrica
d1
= primer dap
d2
= segundo dap
El volumen de los
fustes se generó mediante el empleo del volumen del cilindro, reducido por un
factor mórfico de 0.7:
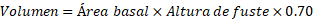
Para el cálculo del error
absoluto se consideró al dap medido con la cinta métrica como el dap real y se
calculó como el valor absoluto de la diferencia entre el dap medido con la
cinta métrica y el dap medido con otro equipo (Diéguez et al. 2003).
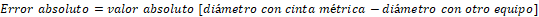
El error relativo se obtuvo del
error absoluto expresado en porcentaje.
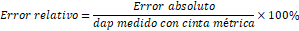
De acuerdo con la recomendación
de Prodan et al. (1997), se obtuvo el coeficiente de correlación de Pearson
entre los dos diámetros que se midieron con la forcípula para analizar el grado
de asociación entre las dos mediciones. Se compararon los diámetros normales
del fuste mediante un análisis de varianza (ANOVA), con diseño de bloques
completamente al azar; donde los tratamientos fueron los métodos como se
obtuvieron los dap y los bloques fueron los árboles. Previamente, la normalidad
de los datos se verificó mediante la prueba de kolmogorov-Smirnov y la
homocedasticidad mediante la prueba de Bartlett (si se comprobó el supuesto de
normalidad) o mediante la prueba de Levene (si no se comprobó el supuesto de
normalidad). Se empleó el logaritmo natural más uno de la variable (con base en
lo sugerido por Steel y Torrie 1988) cuando no se comprobó la normalidad y
homocedasticidad de los datos. Los análisis estadísticos se ejecutaron en el
programa MINITAB (versión 17).
RESULTADOS
Irregularidad de la sección
transversal del fuste
Se analizó el cociente entre los
diámetros que se midieron con la forcípula. Se encontró que Guazuma crinita
tiene una sección transversal muy cercana a la forma circular; con un cociente
entre diámetros normales que varío entre 1.0 y 1.1, para el 78 % de los
árboles. Entre los dos dap medidos con la forcípula de aluminio, también se
obtuvo un coeficiente de correlación de Pearson de 0.936, muy cercano a uno, lo
cual evidenció la fuerte asociación entre los dos dap y, por lo tanto, se
coligió que la sección transversal del fuste fue casi circular.
Diámetro normal del fuste por
equipo
Las medias aritméticas y
medianas, por equipos, no difirieron de manera notoria, pues las medias
aritméticas variaron en décimas o centésimas de centímetro (Cuadro 1). El dap
que se basó en una sola medición con la forcípula fue el que más se diferenció
de los otros métodos (aunque, entre las medianas, las desigualdades fueron
menos notorias). La variabilidad (desviación estándar y coeficiente de
variabilidad) fue similar entre los métodos, donde las desviaciones estándar
variaron en fracciones de centímetro (Tabla 1 y Figura 1).
Tabla 1
Estadísticos
descriptivos del dap.
|
Estadístico
|
CM
|
CD
|
FMA
|
FMG
|
F
|
|
Media
aritmética (cm)
|
17.283
|
17.271
|
17.132
|
17.080
|
16.741
|
|
Mediana
(cm)
|
16.700
|
16.700
|
16.600
|
16.500
|
16.500
|
|
Desviación
estándar (cm)
|
3.233
|
3.244
|
3.237
|
3.233
|
3.174
|
|
Coeficiente
de variabilidad (%)
|
18.7
|
18.8
|
18.9
|
18.9
|
18.9
|
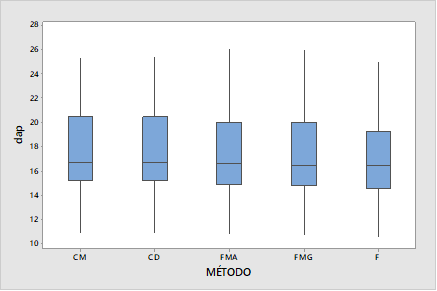
Figura 1:
Gráfica de caja del dap por equipo.
Los coeficientes de correlación
de Pearson evidenciaron la muy fuerte asociación entre los métodos de medición,
pues el grado de la asociación entre la cinta métrica y la cinta diamétrica y
entre el uso de la media aritmética y el uso de la media geométrica fue máximo
(Tabla 2). No obstante, entre la medición de un dap y los otros cuatro métodos,
el grado de la asociación fue claramente menor.
Tabla 2
Coeficientes
de correlación de Pearson para el dap y el volumen.
|
Para el dap
|
|
Método
|
CM
|
CD
|
FMA
|
FMG
|
|
CD
|
1.000
|
|
|
|
|
FMA
|
0.996
|
0.996
|
|
|
|
FMG
|
0.996
|
0.997
|
1.000
|
|
|
F
|
0.978
|
0.978
|
0.983
|
0.982
|
|
Para el volumen
|
|
Método
|
CM
|
CD
|
FMA
|
FMG
|
|
CD
|
1.000
|
|
|
|
|
FMA
|
0.997
|
0.997
|
|
|
|
FMG
|
0.997
|
0.997
|
1.000
|
|
|
F
|
0.989
|
0.989
|
0.989
|
0.991
|
Para el dap, la prueba no
paramétrica de Kolmogorov-Smirnov no verificó el supuesto de normalidad (p <
0.010), ni para el dap transformado por el logaritmo natural más uno (p =
0.025); pero, la prueba de Levene si verificó el supuesto de homocedasticidad (p
= 0.999). No obstante se decidió aplicar el ANOVA sin los datos transformados,
aunque no se verificó el supuesto de normalidad, porque se considera que el
ANOVA es una prueba robusta ante el incumplimiento de los supuestos (Steel y
Torrie 1988, Sokal y Rohlf 2002, Box et al. 2008, Montgomery 2013), porque
todos los tratamientos tuvieron las mismas repeticiones, o sea que el ANOVA
estuvo balanceado (Samuels et al. 2012, Montgomery 2013) y el número de
repeticiones fue grande, con más de 30 unidades experimentales (Samuels et al.
2012). El análisis de varianza para el dap y para el volumen no encontró
diferencias (p = 0.000) entre los tratamientos (el modelo explicó el 99.26 % y
el 99.42 % de la variable de respuesta, respectivamente), en tanto que las pruebas
post-hoc de Tukey y Bonferroni coincidieron en que el dap que se basó en una
medición difirió de los otros tratamientos (Tabla 3).
Tabla 3
Diferencias
entre las medias de los tratamientos para el dap y el volumen.
|
Equipo
|
dap
|
volumen
|
|
Tukey
|
Bonferroni
|
Tukey
|
Bonferroni
|
|
CM
|
a
|
a
|
a
|
a
|
|
CD
|
a
|
ab
|
a
|
a
|
|
FMA
|
ab
|
ab
|
a
|
a
|
|
FMG
|
b
|
b
|
a
|
a
|
|
F
|
c
|
c
|
b
|
b
|
Error de los equipos
Los errores del dap y del volumen
(en ambos casos por árbol) fueron menores cuando el dap se midió con la cinta
diamétrica, pero fueron claramente superiores cuando con la forcípula se midió
un solo diámetro (Tablas 4 y 5). También debe notarse que los errores relativos
del volumen fueron mayores que los del dap.
Tabla 4
Errores
absolutos y relativos del dap por árbol.
|
Estadístico
|
Error absoluto dap (cm)
|
Error relativo dap (%)
|
|
CD
|
FMA
|
FMG
|
F
|
CD
|
FMA
|
FMG
|
F
|
|
Media
aritmética
|
0.027
|
0.234
|
0.266
|
0.712
|
0.2
|
1.3
|
1.5
|
4.0
|
|
Mediana
|
0.000
|
0.200
|
0.200
|
0.600
|
0.0
|
1.1
|
1.4
|
3.8
|
Tabla 5
Errores
absolutos y relativos del volumen por árbol.
|
Estadístico
|
Error absoluto volumen (m3/árbol)
|
Error relativo volumen (%)
|
|
CD
|
FMA
|
FMG
|
F
|
CD
|
FMA
|
FMG
|
F
|
|
Media
aritmética
|
0.00183
|
0.00885
|
0.00963
|
0.02444
|
0.6
|
2.8
|
3.2
|
7.9
|
|
Mediana
|
0.00000
|
0.00800
|
0.00900
|
0.01800
|
0.0
|
3.0
|
3.7
|
8.0
|
|
|
|
|
|
|
|
|
|
|
Con respecto a los volúmenes del
fuste por hectárea, no se encontraron diferencias entre los volúmenes cuando
los dap se midieron con cinta diamétrica y cinta métrica, pero las
desigualdades crecieron gradualmente cuando los diámetros se obtuvieron con la forcípula,
con una diferencia de 7.7 m3/ha cuando se mide un solo dap con la forcípula, un
error que representa 1694 pies tablares aserrados de madera por hectárea,
cantidad muy importante de considerar desde el punto de vista industrial y
financiero (Tabla 6).
Tabla 6
Error
absoluto del volumen por hectárea.
|
Estadístico
|
CM
|
CD
|
FMA
|
FMG
|
F
|
|
Volumen
de la plantación (m3/ha)
|
113.8
|
113.9
|
111.9
|
111.2
|
106.1
|
|
Error
absoluto (m3/ha)
|
|
-0.1
|
1.9
|
2.6
|
7.7
|
|
Error
relativo (%)
|
|
0.0
|
1.7
|
2.3
|
6.8
|
DISCUCIÓN
Este estudio halló que, en
plantaciones de Guazuma crinita “bolaina blanca”, el diámetro de los
árboles se puede medir directamente o medir la circunferencia y de esta última
obtener el dap; respaldando la afirmación de Philip (1994) pero discrepando con
Diéguez et al. (2003), dado que no se halló que sea una ventaja la medición de
la circunferencia con respecto a la medición de dos diámetros con la forcípula.
Empero, tal como aseveran Diéguez et al. (2003) y Philip (1994) el uso de la
forcípula conlleva la obligatoriedad de medir dos diámetros y generar una
media, ya sea aritmética o geométrica.
En este estudio se halló una
contradicción entre los análisis descriptivos y los análisis inferenciales,
pues aunque las medias y medianas de los dap no se diferenciaron notoriamente,
el ANOVA halló diferencias estadística. No obstante, se advirtió que en la
variabilidad se concentró en los árboles (o bloques) y no en los tratamientos
(o equipos), de lo cual se coligió que cometió un error tipo I, o sea que se
rechazó la hipótesis nula (no hubo diferencias entre los tratamientos) siendo
verdadera. Al respecto Samuels et al. (2012) y Sokal y Rohlf (2002) advierten
sobre la posibilidad de obtener conclusiones espurias cuando la variabilidad
debida al error experimental supera a la variabilidad debida a los
tratamientos. Por lo tanto, de los análisis descriptivos e inferenciales se
razonó que, de manera notable, el método de medir un solo dap con la forcípula,
se diferencia de los otros tratamientos; lo cual sería coherente con la
revisión de la literatura pertinente.
Con respecto a los errores
relativos, no debe extrañar que sea mayor con el volumen que con el dap, pues
el cálculo del volumen tiene al dap como un componente más, este resultado es
consistente con la aseveración de Prodan et al. (1997), quienes afirman que el
error relativo en el área basal es el doble del error relativo del diámetro
normal.
Este estudio halló que, con base
en el análisis de la precisión y de los errores, para la medición correcta del
diámetro normal del fuste, de Guazuma crinita, hasta una edad de 13 años
(que supera el turno, rotación o edad de corta), en una plantación (y
presumiblemente en un bosque secundario); se puede optar por el uso de la cinta
métrica, la cinta diamétrica o, indistintamente, el cálculo de una media a
partir de dos dap cuantificados con la forcípula; por lo tanto se difiere con
Rondeux (2010), Silva et al. (2005) Diéguez et al. (2003), Prodan et al.
(1997), Alder y Synnott (1992), Synnott (1991) y Cailliez (1980) quienes alegan
que la cinta métrica es más precisa que la forcípula.
Aunque se corroboró que la cinta
métrica y la cinta diamétrica tienden a sobreestimar el dap, lo cual afirman
Diéguez et al. (2003), Philip (1994), Avery y Burkhart (1994), Cailliez (1980);
la sobrestimación es pequeña y se puede desestimar. Se coincidió con Costa et
al. (2018), Corte et al. (2016) y Freitas y Wichert (1998) para quienes no hay
diferencias estadísticas entre el uso de la cinta métrica, la cinta diamétrica
y la forcípula, para especies nativas y exóticas tropicales establecidas en
plantaciones puras.
Es pertinente considerar que no
se perdió consistencia en las mediciones con la forcípula, porque las efectuó
la misma persona; lo cual, como afirman Campos y Leite (2009) y Rondeux (2010),
es un procedimiento que contribuye a disminuir las diferencias con respecto a
las mediciones con las cintas métrica y diamétrica.
Se agrega que el empleo de la
media aritmética y la media geométrica fue indistinto cuando se midieron dos
dap con la forcípula, lo cual se debió a la circularidad de la sección
transversal del fuste de Guazuma crinita.
Los errores absolutos, en
términos de metros cúbicos por hectárea, que se hallaron cuando se miden los
diámetros con forcípula fueron notoriamente importantes, que variaron entre 1.9
y 7.7 metros cúbicos por hectárea, equivalentes a 418 y 1694 pies tablares
aserrados, una cantidad definitivamente a considerar desde el punto de vista
industrial y financiero.
CONCLUSIONES
Para árboles plantados de Guazuma
crinita, producidos de semilla de diferentes procedencias, cuyas secciones
transversales del fuste son próximas a la circularidad completa; se concluye
que el diámetro normal del fuste se puede medir, sin distinción, con cinta
métrica, cinta diamétrica o forcípula de aluminio; pero, en este último caso,
se deben medir dos diámetros y promediarlos, de manera indistinta, con la media
aritmética o media geométrica.
Los errores con cinta diamétrica
y forcípula de aluminio, con respecto a la cinta métrica son bajos. Pero, los
errores son conspicuos cuando se calculan a nivel de volumen de madera por
hectárea. Empero, la selección del equipo para medir el dap obedecerá a la
calidad de la medición que se imponga el interesado y el error que la autoridad
forestal permita.
REFERENCIAS BIBLIOGRÁFICAS
[1]
Alder, D; Synnott, TJ. 1992. Permanent sample
plot techniques for mixed tropical forests. Oxford, UK, Oxford Forestry
Institute. 124 p.
[2] Avery, TE; Burkhart, HE. 1994. Forest measurements. 4 ed. New York,
USA, McGraw-Hill. 408 p.
[3] Box, GE; Hunter, JS; Hunter, WG. 2008. Estadística para
investigadores. Diseño, innovación y descubrimiento. 2 ed. Barcelona, España,
Reverté. 639 p.
[4] Cailliez,
F. 1980. Estimación del volumen forestal y predicción del rendimiento:
estimación del volumen. Roma, Italia, FAO. 92 p.
[5] Campos,
JCC; Leite, HG. 2009. Mensuração florestal. 3ed. Viçosa, Brasil, Editora UFV.
548 p.
[6] Corte
D, AP; Sanquetta, CR; Oliveira, KA de; Behling, A; Coutinho M, V. 2016.
Desempenho de diferentes equipamentos para mensuração de diâmetro a 1,30 m,
altura individual total, e volume do fuste em Cryptomeria japonica (Thunb. ex
L. f.) D. Don. Enciclopédia Biosfera, 13(23): 432-441.
[7] Costa
M, AC da; Miranda V, RO de; Soares V, AA; Ramos de O, L; Azevedo R, HC de;
Oliveira F, J de; Souza da S, Jaqueline da. 2018. Compatibilidade de diâmetros
de cedro-australiano e mogno africano obtidos por diferentes instrumentos. In
Simpósio de Ciencias Agrárias e Ambientais (VI Simpósio da Agronomia e IV
Simpósio da Engenharia Florestal, 2018, Minas Gerais, Brasil).
[8] Diéguez
A, U; Barrio A, M; Castedo D, F; Ruíz G, AD; Álvarez T, MF; Álvarez G, JG; Rojo
A, A. 2003. Dendrometría. Madrid, España, Ediciones Mundi-Prensa. 327 p.
[9] Freitas G, A; Wichert P, MC. (1998). Comparação entre
instrumentos tradicionais de medição de diámetro e altura com o criterion 400.
Brasil, Instituto de Pesquisas e Estudos Florestais. 4 p.
[10] Guariguata, M; Arce, J;
Ammour, T; Capella, JL. 2017. Las plantaciones forestales en Perú: reflexiones,
estatus actual y perspectivas a futuro. Bogor, Indonesia, CIFOR. 29 p.
[11] López P, C; Ambrosio T, Y.
2009. Dendrometría gráfica. Madrid, España, Universidad Politécnica de Madrid.
98 p.
[12] López P, C; Marchal N, B.
1991. Dasometría práctica. Madrid, España, Universidad Politécnica de Madrid.
149 p.
[13] Malleux, J. 1982.
Inventarios forestales en bosques tropicales. UNALM. Lima, Perú. 414 p.
[14] Masías C, VM. 2017.
Consideraciones para la medición de diámetros y alturas de árboles vivos de
Polylepis flavipila (Bitter) M. Kessler & Schmidt-Leb. Trabajo monográfico
para la obtención del título profesional de ingeniero forestal. 49 p.
[15] Montgomery, DC. 2013. Diseño
de experimentos. 2 ed. D.F., México, Limusa. 686 p.
[16] Moya
C, R. 2005. Estadística descriptiva. 2 ed. Lima, Perú, Editorial San Marcos. 471 p.
[17] Philip, M S. 1994. Measuring trees and forests. Wallingford, UK, CAB
International. 310 p.
[18] Prodan, M;
Peters, R; Cox, F; Real, P. 1997. Mensura forestal. San José, CR, IICA,
BMZ/GTZ. 561 p.
[19] Rondeux, J. 2010. Medición
de árboles y masas forestales. Trad. A Diaz de Barrionuevo. Madrid, España,
Ediciones Mundi-Prensa. 521 p.
[20] Samuels,
ML; Witmer, JA; Schaffner, A. 2012. Fundamentos de estadística para las
ciencias de la vida. Madrid, España, Pearson. 631 p.
[21] SERFOR (Servicio Nacional
Forestal y de Fauna Silvestre, Perú). 2015. Perú forestal en números. Lima,
Perú.
[22] Silva, JN; Lopes, J;
Oliveira, L de; Silva, S da; Carvalho, J de; Costa, D; Melo, M; Tavares, M.
2005. Diretrizes para instalação e medição de parcelas permanentes em florestas
naturais da Amazônia Brasileira. Belem, Brasil, CIFOR, ITTO, EMBRAPA. 68 p.
[23] Soares, CPB; Neto, F; Souza,
AL. 2010. Dendrometria e inventário florestal. Viçosa, Brasil, Universidad
Federal de Viçosa. 276 p.
[24] Sokal, RR; Rohlf, FJ. 2002.
Introducción a la bioestadística. Barcelona, España, Reverté. 362 p.
[25] Steel, RG; Torrie, JH. 1988.
Bioestadística: principios y procedimientos. 2 ed. D.F., México, McGraw-Hill.
622 p.
[26] Synnott, T J. 1991. Manual
de procedimientos de parcelas permanentes para bosque húmedo tropical. Trad. J
Valerio. CR, Instituto Tecnológico de Costa Rica. 103 p.
[27] Universidad Nacional de Ucayali
– UNU. 2008. Estación meteorológica. Datos climáticos de ocho años en la zona
de Pucallpa, Perú.
[28] Wabö, E; Cellini, JM;
Martínez Pastur, G; Lencinas, MV. 2007. Comparación entre la exactitud relativa
de la forcípula y de la cinta diamétrica en la determinación del DAP, el área
basal y el volumen, Quebracho no.14:5-14.